La statistica – non soltanto in economia – è una brutta bestia. Ma esiste una certezza, mai ripetuta abbastanza: correlazione non significa causazione. Osservi un fenomeno, al verificarsi di alcuni eventi (X) segue (si correla) il verificarsi di altri eventi (Y). Allora X ha causato Y?
NO
Questa osservazione non è sufficiente. Come fai a dire se è X che ha causato Y, o non piuttosto qualcos’altro? O magari è Y che ha causato X?
Osserviamo che nei giorni di pioggia molte persone portano l’ombrello: c’è un’alta correlazione tra le due variabili. Potremmo aprire un blog di informazione alternativa e dire alla gente di aprire gli occhi, perché c’è un complotto che funziona così: gli ombrelli causano la pioggia e per colpa degli ombrelli che causano la pioggia tanta gente rimane a casa a farsi indottrinare dalla TV di regime. Per fortuna, in questo caso la scienza ha dimostrato che la pioggia non è causata dagli ombrelli. La logica della scienza, infatti, prevede un semplice modo per testare la teoria che gli ombrelli causino la pioggia: gli esperimenti empirici. Se molte persone si trovassero in piazza in un giorno di sole e provassero a aprire i loro ombrelli, e l’esperimento fosse ripetuto un numero adeguato di volte, allora la statistica mostrerebbe con confidenza estrema che, a parte la casualità sempre possibile della pioggia che cade all’apertura degli ombrelli, l’evento pioggia non è causato dalla danza degli ombrelli al sole. Blog di questo tipo non possono avere (forse) successo.
In un laboratorio di fisica gli esperimenti empirici sono facili, perché si può operare in condizioni ideali, eliminando tutte le “variabili confondenti“, in cui ogni ripetizione dello stesso esperimento porta sempre agli stessi risultati, a meno dell’errore di misurazione.
Anche in medicina è talora possibile effettuare degli esperimenti veri e propri, sfruttando i “gruppi di controllo in doppio cieco”: soggetti statisticamente esposti a tutte le altre variabili ipotizzabili, ma non al principio attivo del farmaco: se si scopre che è molto improbabile che le differenze di sopravvivenza tra il gruppo che riceve il farmaco e il gruppo di controllo siano frutto del caso, allora è stato il farmaco. In altri casi invece, un esperimento così non è praticabile, o ciò che si vuole studiare è ad esempio un fattore di rischio, qualcosa a cui eticamente o praticamente non puoi sottoporre volontariamente le persone, e si usano gli studi prospettici, si analizzano le curve di sopravvivenza della popolazione di chi è stato esposto a un fattore di rischio, e così via.
Purtroppo, in economia non puoi fare (quasi mai) esperimenti in condizioni controllate e comparabili. Quindi devi andarti a studiare cosa è successo storicamente, tutte le possibili variabili, e cercare il modello che spiega meglio il fenomeno, tramite strumenti quali la regressione multipla, e cercare di avvicinarsi il più possibile a un esperimento empirico. Altrimenti è esattamente come vedere gli ombrelli aprirsi e maledire i passanti perché causano la pioggia.
Non è quindi solo una questione matematica, ma interpretazione dei fenomeni secondo strumenti e modelli dati dalla scienza economica, alla luce dell’analisi statistica. Le correlazioni spurie che raccogliamo in questo sito sono statisticamente valide, quanto ovviamente stupide.
Vediamo come si costruisce una teoria e la si prova, nei vari passaggi, e perché serve una testa, meglio pensante, per interpretare un grafico.
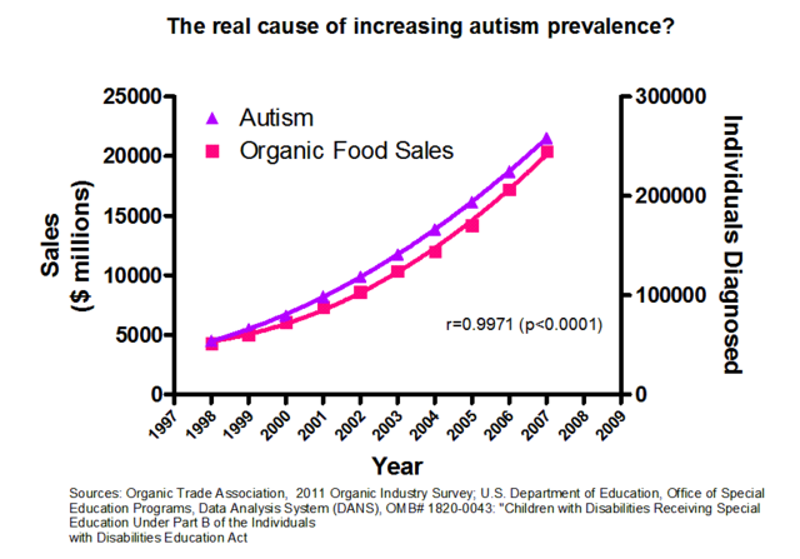
Un caso molto chiaro di due variabili strettamente correlate (p<0.0001), in cui ovviamente non c’è correlazione alcuna.
Approfondimento
È sufficiente osservare una correlazione tra due variabili X e Y per dire che X ha effetti su Y? 1
Se fossero possibili esperimenti su X -verificando che succede a Y- la correlazione significativa trovata nei dati sarebbe già conclusiva. Ma non sempre ciò è possibile. L’esempio tipicamente usato è quello di stimare gli effetti degli anni di istruzione sul salario futuro.
Domanda: di quanto aumenta il tuo salario annuo se vai a scuola un anno in più? Una risposta immediata l’avresti da un esperimento. Ma chi osa assegnare a caso gli anni di istruzione alle persone? Tu preso a caso studi 10 anni, tu 15, tu 2!
Dato che non puoi effettuare un esperimento devi trovare altre strade più impervie. Devi arrivare vicino a un esperimento. Il problema sono le variabili omesse, cioè le variabili che sono correlate sia con l’istruzione sia con il salario. Esempi?
La posizione economica dei genitori è un esempio di variabile omessa, oppure l’abilità della persona. Perché? Se sei un tipo sveglio avrai meno difficoltà ad apprendere a scuola. E probabilmente sei anche sveglio sul lavoro. La variabile omessa “abilità” è correlata positivamente sia con gli anni di istruzione che con il salario futuro.
Detto in altri termini: la variabile omessa “abilità” confonde le acque perché si muove insieme alle altre due, ma non la osservi. Se guardi solo correlazione tra anni di istruzione e salario futuro senza tener conto dell’abilità, rischi di sopravvalutare l’effetto causale dell’istruzione sul salario. La ragione è che l’istruzione “ti assorbe” l’effetto dell’abilità. Individui più abili studiano per più anni e guadagnano di più. Ma tu pensi che quel guadagno in più sia tutto dovuto all’istruzione! Individui più abili studiano per più anni e guadagnano di più. Ma tu pensi che quel guadagno in più sia tutto dovuto all’istruzione!
Non basta mostrarti un grafico dove si vede che è successo qualcosa, per poi ammiccare a quel che succede dopo!
Per non farti ingannare dai dati, devi tenere conto delle variabili omesse. Come? Maniera più semplice: raccogli dati su quelle variabili. Puoi misurare il QI (un’approssimazione del livello di abilità) delle persone e passare dalla semplice correlazione a un modello di regressione multipla. La regressione multipla, in questo caso, consiste nel guardare il legame esistente tra anni di istruzione e salario a pari livello di abilità. È come se prendessi tizi a pari livello di abilità (variabile che dunque non ti confonde più) e analizzassi salario e anni di istruzione.
Certo sarebbe un mondo molto più facile se potessi fare esperimenti e guardare solo un grafico con due variabili. Tuttavia nei fenomeni macroeconomici è quasi impossibile fare un esperimento. Quindi le variabili omesse sono il principale pericolo. Dunque non basta mostrarti un grafico dove si vede che è successo qualcosa, per poi ammiccare a quel che succede dopo!
Dato che l’evento x non è un esperimento – cioè non è fatto in maniera casuale – un grafico non ti dice niente.
Un grafico, da solo non dimostra nulla
Soprattutto, non sappiamo cosa sarebbe successo se l’evento non fosse accaduto. Manca il controfattuale. All’aumento della spesa pubblica segue una più alta crescita? Può darsi che questa accelerazione si sarebbe verificata comunque, a causa di altri motivi che stiamo ignorando.
Secondo tentativo (sempre da furbastri): ti faccio vedere due paesi, uno colpito dall’evento e uno no, e ti mostro la differenza. Ma… ancora una volta non è esperimento (che un paese sia colpito da un evento e l’altro no, di solito non è frutto di un esperimento, sarà sfiga, sarà quello che volete, ma non di un esperimento).
Prima conclusione: se non c’è un esperimento (o qualcosa che “ci assomiglia”) un grafico non dimostra assolutamente nulla.
Buttiamoci ordunque sull’euro: chi ti mostra un grafico con l’andamento di paesi dentro e fuori dall’euro non ti dimostra nulla. Perché non dimostra nulla? Perché non basta ciò per convincermi che stai analizzando qualcosa che assomiglia a un esperimento.
Diciamolo: dal punto di vista statistico le variabili omesse sono i serial killer di chi ti vuole dimostrare qualcosa con un grafico.
Passiamo a un tema connesso: il secondo serial killer degli imbonitori di statistica a buon mercato è il concetto di endogeneità. In breve: se vuoi dimostrare gli effetti di X su Y, attento che Y potrebbe avere effetti su X! Endogeneità o causalità inversa.
Chi – in assenza di esperimenti – ti vuole dimostrare qualcosa con un grafico non sa la statistica o è in cattiva fede.
Torniamo a bomba. Chi se ne fotte dell’endogeneità se hai un esperimento? Distribuisci a caso la variabile X e vedi l’effetto sulla Y. Ecco a voi un esempio: vuoi studiare gli effetti della protezione dei diritti di proprietà (X) sulla crescita economica (Y). L’idea teorica alla base è che – se i diritti di proprietà sono protetti – la gente ha più voglia di investire e la produzione aumenta.
Supponi di guardare dati macroeconomici. Eccoti la causalità inversa: un paese più ricco può proteggere meglio i diritti di proprietà. Perché mai? Be’, perché l’ordine pubblico e il sistema giudiziario costano, e non tutti i paesi possono finanziarli per bene.
Se trovi nei dati una correlazione positiva tra PIL pro capite e protezione dei diritti di proprietà che cosa concludi? Boh! Forse la protezione dei diritti di proprietà rende un paese più ricco oppure un paese più ricco può permettersi protezione. O entrambe!
In termini tecnici: ancora una volta una correlazione non ti dice assolutamente niente di conclusivo sui rapporti causali sottostanti. Chi – in assenza di esperimenti – ti vuole dimostrare qualcosa con un grafico non sa la statistica, o è in cattiva fede.
- Quella che segue è una rielaborazione di una serie di Tweet del Prof. Riccardo Puglisi, professore associato di Economia all’Università di Pavia. La pagina contiene contributi di Carlo Piana e Claudio Baccianti.↩
